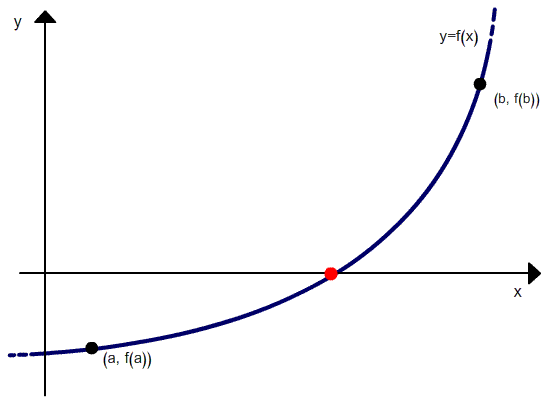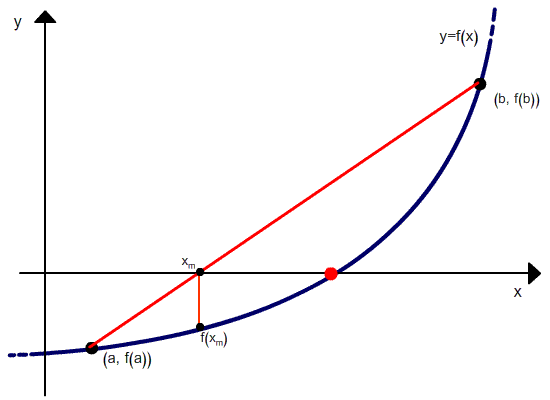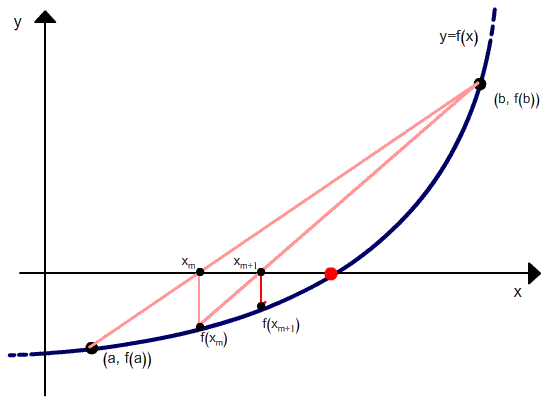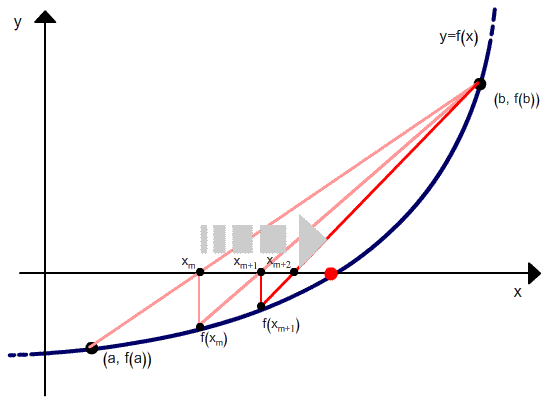
Regula Falsi Method: The convergce process in the bisection method is very slow. It depends only on the choice of end points of the interval [a,b]. The function f(x) does not have any role in finding the point c (which is just the mid-point of a and b). It is used only to decide the next smaller interval [a,c] or [c,b]. A better approximation to c can be obtained by taking the straight line L joining the points (a,f(a)) and (b,f(b)) intersecting the x-axis. To obtain the value of m we can equate the two expressions of the slope m of the line L.
Algorithm :
For any continuous function f(x),

• Find two points, say a and b such that a < b and f(a)* f(b) < 0 and initialize error e (depends upto what accuracy you want the result)
• Take the interval [a, b] and determine the next value of m.
m = [a*f(b)-b*f(a)] / [f(b)-f(a)]
• m is the root of the given function if f(m) = 0; else follow the next step
• If f(a)*f(m) > 0 then a = m
else b = m
• Repeat above steps until |f(m)| < e.