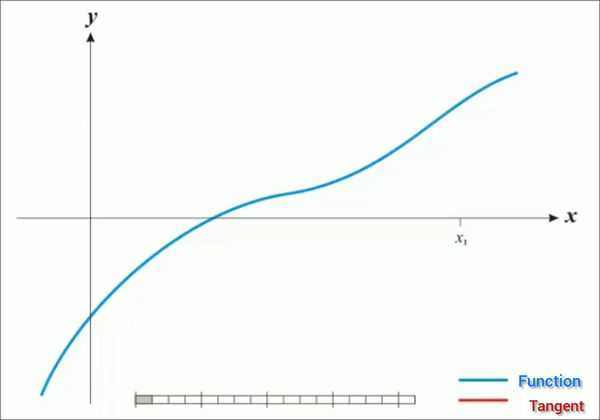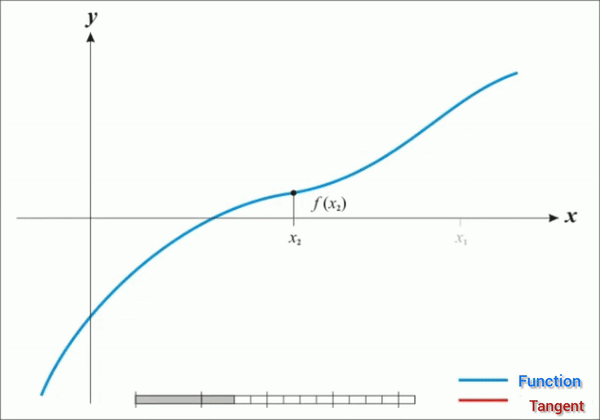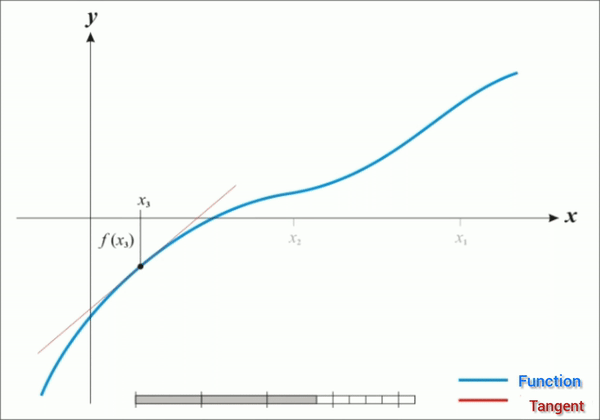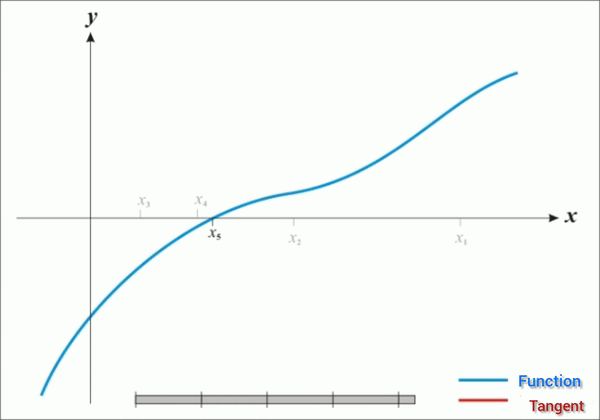
Newton's Method : - Newton's Method is also called the Newton-Raphson method is a recursive algorithm for approximating the root of a differentiable function f(x)=0. It is based on the geometry of a curve, using the tangent lines to a curve. As such, it requires calculus, in particular differentiation.
Algorithm :
For any continuous function f(x),

• Guess a initial value, say b and initialize error e (depends upto what accuracy you want the result)
• find m = b-(f(b)/f'(b))
• m is the root of the given function if f(m) = 0 then stop else follow the next step
• b = m
• m = b-(f(b)/f'(b))
• Repeat 3, 4, 5 step untill |f(m)|<e.