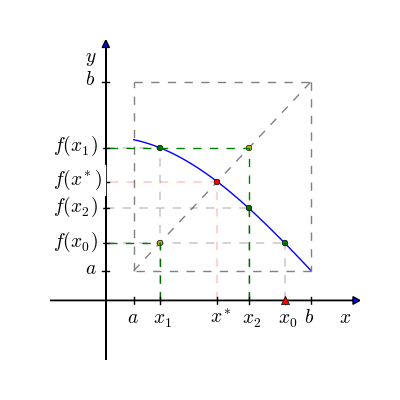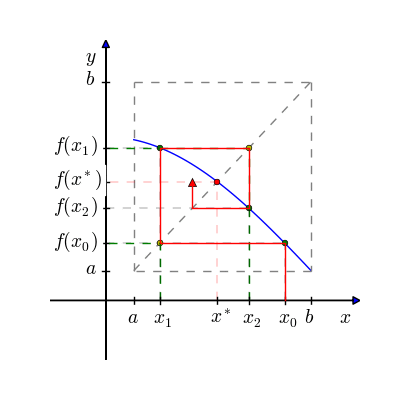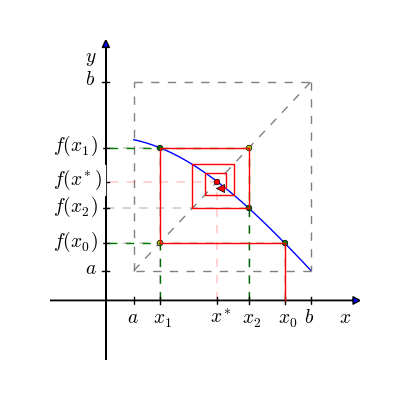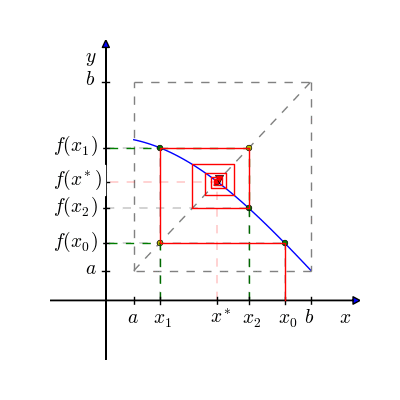
Fixed Point Iteration Method: Fixed point iteration method is open and simple method for finding real root of non-linear equation by successive approximation. It requires only one initial guess to start. Since it is open method its convergence is not guaranteed. This method is also known as Successive Approximation Method. To find the root of nonlinear equation f(x)=0 by fixed point iteration method, we write given equation f(x)=0 in the form of x = g(x). If x0 is initial guess then next approximated root in this method is obtaine by: x1 = g(x1) And similarly, next to next approximated root is obtained by using value of x1 i.e. x2 = g(x2) And the process is repeated until we get root within desired accuracy e.
Algorithm :
For any continuous function f(x),

• Guess a initial value, sa y b and initialize error e (depends upto what accuracy you want the result)
• write f(x)=0 in the form x=g(x)
m = g(b)
• m is the root of the given function if f(m) = 0 then stop else follow the next step
• b = m
• Repeat step 3, 4 until |f(m)| < e.