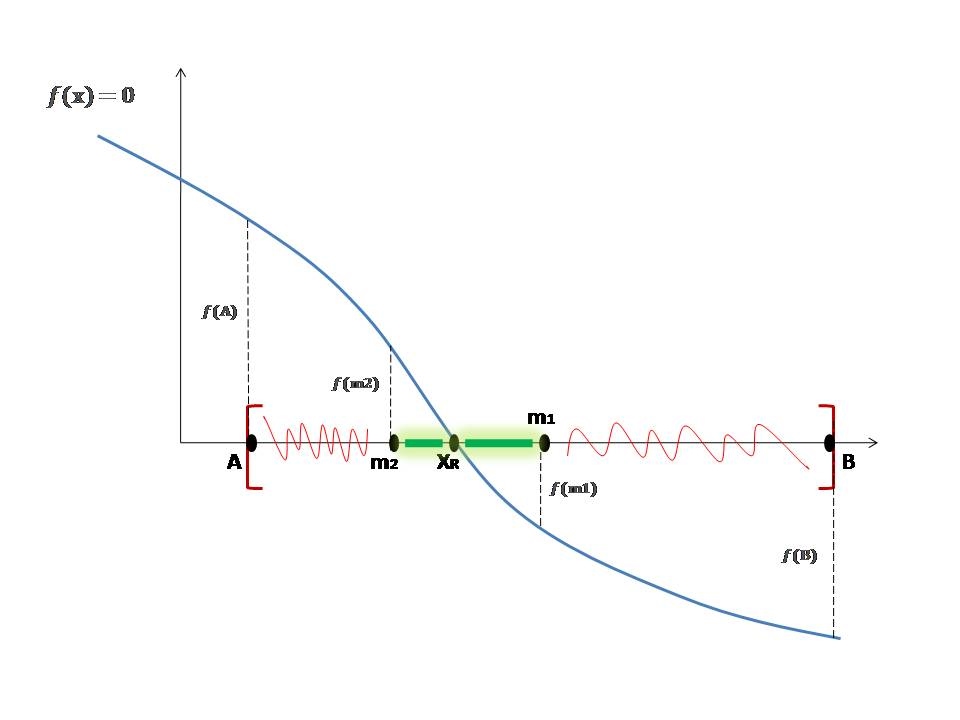
In the field of numerical methods, the Euler method (also called forward Euler method) is a first-order numerical procedure for solving ordinary differential equations (ODEs) with a given initial value. It is the most basic explicit method for numerical integration of ordinary differential equations. Consider a differential equation dy/dx = f(x, y) with initialcondition y(x0)=y0 then succesive approximation of this equation can be given by:

• y(n+1) = y(n) + h * f(x(n), y(n))
• where h = (x(n) – x(0)) / n

h indicates step size. Choosing smaller values of h leads to more accurate results and more computation time.